وبلاگ پایه ششم دبستان
إِنَّا خَلَقْنَا الْإِنْسَانَ مِنْ نُطْفَةٍ أَمْشَاجٍ نَبْتَلِیهِ فَجَعَلْنَاهُ سَمِیعًا بَصِیرًا
قال الله تعالی: «إنّا نحنُ نَزّلنا الذِّکرَ و انّا له لَحافِظون» (حجر / 9)
إِنَّا هَدَیْنَاهُ السَّبِیلَ إِمَّا شَاکِرًا وَإِمَّا کَفُورًا
- ۹۶/۱۰/۲۳تبدیل واحد در اندازه گیری ششم
- ۹۶/۱۰/۰۲مرکز تقارن و تقارن مرکزی
- ۹۶/۰۹/۰۴الگو
- ۹۶/۰۹/۰۴الگو مخمسی و مسدسی
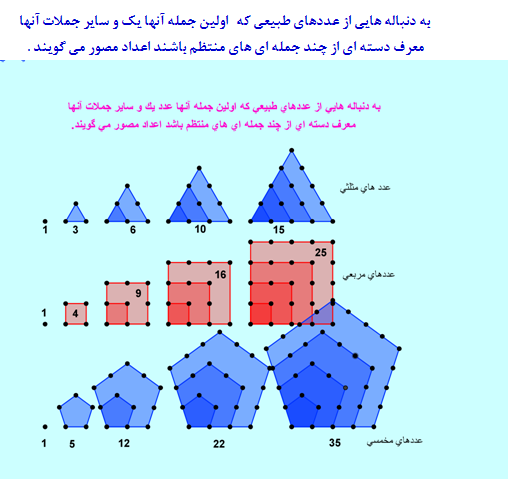
- ۹۶/۰۹/۰۴اعداد مصور
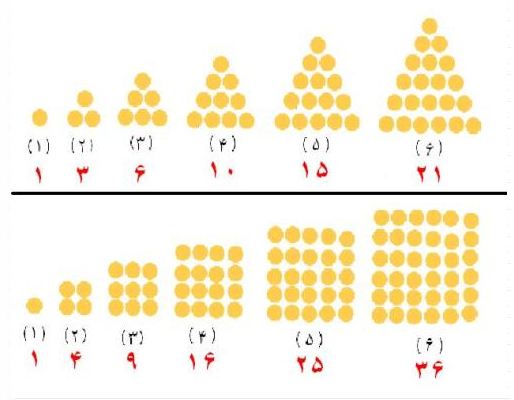
- ۹۶/۰۹/۰۴الگو مثلثی و مربعی
- ۹۵/۱۱/۲۳شیر خدا
- لینک خرید شارژ ، بسته اینترنتی و پرداخت قبض
- حافظه ی دیداری
- مشکلات ویژه یادگیری
- اختلال کودکان
- زنگ ریاضی ( آموزش مفاهیم ریاضیات )
- تلاوت استاد شحات انور
- ترتیل منشاوی
- کتاب گویای قرآن ششم ابتدایی
- قرآن با صدای استاد ماهر المعیقلی
- صدای سعد الغامدی
- قران با صدای استاد خلیل الحصری
- تلاوت های استاد راغب مصطفی غلوش
- قرآن با صدای مشاری بن راشد العفاسی
اعداد مخمسی نیز عبارتند از: ۱،5،12،22،35،51،70،92،117،145،176، ... ریاضیدانان محاسبه کردهاند، که در اینجا نیز با معلوم بودن شمار دکمهها در یک ضلع، تعداد دکمههای به کار رفته درکل آن معلوم میگردد، کافی است، شمار دکمههایی را که در یک ضلع واقعند، ضرب در خودشان کنیم، و آن را با تمام اعداد طبیعی و متوالی پایینتر از خود جمع کنید. مثلاً محاسبهی دکمههای به کار رفته در آخرین پنج ضلعی جدول چنین است: ۱+۲+۳+۴+۵۲، که مساوی ۳۵میشود. و هر گاه بخواهیم یک عدد مخمسی پیدا کنیم، که یک ضلع شامل ۸ واحد شود، باید چنین کنیم: ۱+۲+۳+۴+۵+۶+۷+۸۲که حاصل ۹۲میشود.
روش یافتن اعداد مثلثی : این فرمول ساده را به ذهن بسپارید،
2 ÷ [ (1+ شماره ی شکل ) × شماره ی شکل ].
برای مثال عدد مثلثی شماره ی 4 به این روش به دست می آید: 10 = 2 ÷ ( 5 × 4 ).
روش یافتن اعداد مربعی بسیار آسانتر است. کافی است مساحت مربعی را بیابید که شماره ی شکل، ضلع آن است.
برای مثال: عدد مربعی شماره ی 4 به این روش به دست می آید: 16 = 4 × 4 .